
Zadanie Kwadrat magiczny (kwa)
Pomóż nam usprawnić bazę zadań!
Kwadrat magiczny
Limit pamięci: 32 MB
Bajtazar znalazł w swojej piwnicy bardzo stare pudełko. Gdy je otworzył, zobaczył wielką stertę tajemniczych tabliczek z wypisanymi na nich liczbami. Oto jedna z nich:

Już po chwili Bajtazar zauważył, że jest to kwadrat magiczny!
Każdy taki kwadrat jest bowiem tabelką rozmiaru 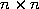 , do której wpisano
, do której wpisano
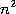 różnych liczb całkowitych dodatnich
o tej własności, że suma liczb w każdym wierszu, w każdej kolumnie i na każdej
z dwóch przekątnych jest taka sama.
W powyższym kwadracie wszystkie wiersze, kolumny i przekątne sumują się do
różnych liczb całkowitych dodatnich
o tej własności, że suma liczb w każdym wierszu, w każdej kolumnie i na każdej
z dwóch przekątnych jest taka sama.
W powyższym kwadracie wszystkie wiersze, kolumny i przekątne sumują się do  .
.
Ucieszony tym odkryciem, Bajtazar zabrał się za przeglądanie innych tabliczek. Niestety na
wielu z nich liczby były zatarte. Po dokładniejszych oględzinach zauważył, że zawsze brakuje
zawartości pewnych  pól, z których żadne dwa nie znajdują się w jednym wierszu ani w jednej kolumnie.
Bajtazar uwielbia zagadki matematyczne, ale nie jest dobry w ich rozwiązywaniu.
Czy potrafisz pomóc mu uzupełnić zawartości brakujących pól tak, aby tabliczka znów stanowiła
kwadrat magiczny?
pól, z których żadne dwa nie znajdują się w jednym wierszu ani w jednej kolumnie.
Bajtazar uwielbia zagadki matematyczne, ale nie jest dobry w ich rozwiązywaniu.
Czy potrafisz pomóc mu uzupełnić zawartości brakujących pól tak, aby tabliczka znów stanowiła
kwadrat magiczny?
Wejście
Pierwszy wiersz standardowego wejścia zawiera jedną liczbę całkowitą
 (
(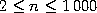 ), oznaczającą rozmiar kwadratu magicznego.
Każdy z kolejnych
), oznaczającą rozmiar kwadratu magicznego.
Każdy z kolejnych  wierszy zawiera po
wierszy zawiera po  liczb całkowitych
liczb całkowitych 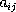 (
(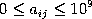 ) pooddzielanych pojedynczymi odstępami;
liczby
) pooddzielanych pojedynczymi odstępami;
liczby 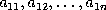 reprezentują zawartość pierwszego
wiersza tabelki, liczby
reprezentują zawartość pierwszego
wiersza tabelki, liczby  zawartość drugiego
wiersza itd.
Dodatnie liczby
zawartość drugiego
wiersza itd.
Dodatnie liczby 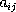 oznaczają zawartość poszczególnych pól
kwadratu magicznego, a zera reprezentują pola, których wartości były zatarte.
oznaczają zawartość poszczególnych pól
kwadratu magicznego, a zera reprezentują pola, których wartości były zatarte.
Wyjście
Twój program powinien wypisać na standardowe wyjście  wierszy, z których
każdy powinien zawierać
wierszy, z których
każdy powinien zawierać  dodatnich liczb całkowitych nie większych niż
dodatnich liczb całkowitych nie większych niż
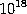 , pooddzielanych pojedynczymi odstępami.
Liczby te mają reprezentować uzupełniony kwadrat magiczny z wejścia.
, pooddzielanych pojedynczymi odstępami.
Liczby te mają reprezentować uzupełniony kwadrat magiczny z wejścia.
Możesz założyć, że dane wejściowe będą tak skonstruowane, że uzupełnienie tabelki do kwadratu magicznego w opisany sposób będzie możliwe. Jeśli istnieje więcej niż jedna poprawna odpowiedź, Twój program może wypisać dowolną z nich.
Przykład
Dla danych wejściowych:
4 0 35 34 4 32 0 7 29 8 30 31 0 33 3 0 36
poprawną odpowiedzią jest:
1 35 34 4 32 6 7 29 8 30 31 5 33 3 2 36
Autorzy zadania: Marian M. Kędzierski, Tomasz Kulczyński.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English